
Rather than having to create a normal distribution curve for every possible dataset, we can just use one standard normal distribution curve and use set formulas to find probabilities.īut the real beauty behind z scores is found in how we calculate probability.

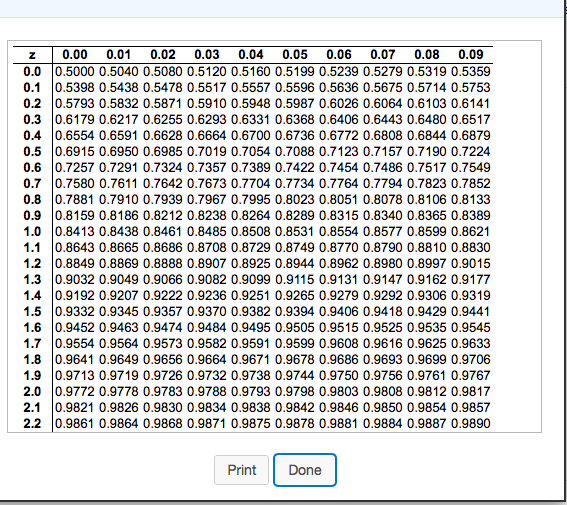
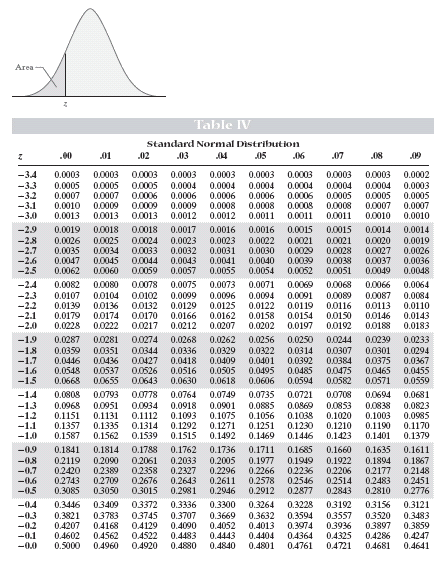
Standard Normal Distribution and Z Scores In other words, a Z score is the number of standard deviations from the mean value and tells you where the scores lie on a normal distribution curve, as Statistics How To nicely states. So a Z-score of 1 is 1 standard deviation above the mean and a Z score of -1 is 1 standard deviation below the mean. First, we let the mean become zero (centered around the y-axis) and the z scores represent the standard score, similar to the standard deviations to the left and right of the mean. The z score is used when we standardize a bell curve. However, sometimes the data doesn’t cooperate, and we need to find the probability of an outcome that does not fall directly within 1, 2, or even 3 standard deviations from the mean. The easiest way to find these values is by using the Empirical Rule, as we saw in our previous lesson. We calculate the probability or the likelihood an outcome will occur, by determining the area under the normal distribution curve, or bell curve. And the standard deviation helps us to measure the spread or distance the data is from the mean.
The spread, or distribution, has symmetry around the center or mean, and 50% of the data falls to the left of the center and 50% of the data falls to the right. Well, if data tends to be around one central value then we say it is normally distributed. Or what the difference is between a z score and the standard deviation? Jenn, Founder Calcworkshop ®, 15+ Years Experience (Licensed & Certified Teacher)


 0 kommentar(er)
0 kommentar(er)
